TX00CQ31 – Digital Signal Processing

Study 4: Poles and Zeros


Read these instructions first!

Number

Questions

 
Write your answer in this column

Hints

Q1

System difference equation is

       y[n] – 0,4y[n-1] = x[n] – 0,5x[n-1] + 0,06x[n-2]

 

Describe the system parameters such that you can use them in Octave/Matlab

Commands:

n = -10:100;

x = n >= 0;

aa = [1,-0.4,0];       % X(z) = 1 - 0.5 * z^-1 + 0.06 * z^-2

bb = [1,-0.5,0.06];     % Y(z) = 1 - 0.4 * z^-1 + 0 * z^-2

y = filter(bb,aa,x);

see lab 2, how you put those system  parameters to the filter command

Q2

Draw Argand’s diagram (=zero-pole plot) and determine if the system is stable or not.

stem plot

 

Is the system stable?

Yes, because all the poles reside inside the unit circle.

zplane()

Q3

Calculate the zeros and poles of the system.

Commands:

zz = roots(bb)

zz = 0.3000  0.2000

pp = roots(aa)

pp = 0.4000  0

roots()

Q4

Generate Frequency Response using sampling rate of 22050 s-1

 stem plot

freqz()

Q5

Determine if the system is IIR or FIR by testing it with impulse function.

IIR/FIR, why?

FIR, because by time the output value tends to return to zero (after 822 samples).

filter()

Q6

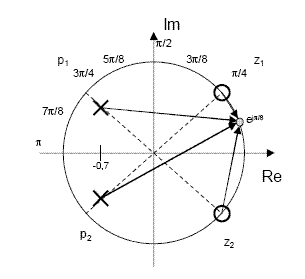
A second degree system has the following zero-pole plot.

Determine the zero and pole coordinates.

Zeros are…

zz = 0.7071 + 0.7071i

  0.7071 - 0.7071i

Poles are…

pp = -0.7000 + 0.7000i

  -0.7000 - 0.7000i

and that can be verified from this picture…

Yes, it matches up with the locations of the zeros and poles that the picture implies.

stem plot

[ ; ]

Q7

Determine the corresponding system parameters (in Octave/Matlab form).

Commands:

aan = poly(ppn)

aan = 1.0000 1.4000 0.9800

bbn = poly(zzn)

bbn = 1.0000 -1.4142 1.0000

The difference equation: y[n]+ 1,4y[n-1] + 0,98y[n-2] = x[n] -1.412x[n-1] + x[n-2]

poly

Q8

Determine the maximum gain and rescale the system such that it has unity gain passband.

 

Generate Frequency Response to verify it.

stem plot

freqz

Q9

Just for fun, filter a white noise audio sample with the filter and describe how your system changes the signal. Use a reasonable sampling rate (8000, 11025, 22050, 44100) in your test.

Commands:

n = -10:1000;

x = n >= 0;

for i = 1:length(n)

q(i) = rand();

end

noisy_signal = x .* q;

noise_output = filter(bbns,aan,noisy_signal)

stem plot

White noise: try randn()