Lainalaskelmia

Johdanto

Eräänä päivänä asunnon ostaminen tulee ajankohtaiseksi. Tällaisen ison ostoksen kanssa pitää pohtia monia asioita ennen ostopäätöstä, kuten millaista asuntoa hakee, kuinka paljon on mahdollista ottaa lainaa ja kuinka paljon kuukausieräksi tällöin muodostuu. Lisäksi on syytä miettiä, kuinka pitkän lainan on valmis ottamaan. Nykyään, kun tarvitaan suuria lainasummia, näyttäisi olevan varsin tavallista ottaa pankista pitkiä, 25 - 30:n vuoden lainoja.

Tavalliset lainatyypit ovat ns. tasalyhennys- ja tasaerälaina. Tasalyhennyslainassa laina jaetaan samansuuruisiin lyhennyksiin ja lainan korko lasketaan lainan päälle. Näin ollen alkuvaiheessa, kun pääoma ei ole ehtinyt lyhentyä paljoa, lainan kuukausierät (lyhennys + korko) saattavat olla varsin suuria. Loppuvaiheessa taas erät ovat pienempia. Tällainen lainamuoto sopiikin paremmin pienikorkoisille varsin pienille lainasummille. Esimerkiksi opintolaina on usein tällainen ns. tasalyhennyksin lyhennettävä.

Tasaerä- eli annuiteettilainassa taas kuukausierä on koko ajan saman suuruinen. Lainan koron ja lyhennyksen suhde vaihtelee. Tällaisella menetelmällä pyritään siihen, etteivät lainan lyhennykset kuormittaisin alkuvaiheessa kohtuuttomasti lainan maksajaa ja tällainen laina sopiikin sen takia paremmin pitkiin ja lainamäärältään suuriin lainoihin. Esimerkiksi asuntolainat ovat yleensä juuri tällaisia annuiteettilainoja. Jos korko muuttuu laina-aikana, kuukausierä elää lainan mukana, eli siis nousee taikka laskee.

Annuiteettilainan eräs muoto on laina, jossa kuukausierä sovitaan kiinteäksi. Tällöin, jos lainan korko nousee, laina-aika pitenee, vastaavasti koron laskiessa laina-aikakin lyhenee. Tällaisessa lainassa on aina se vaara, että jos korot nousevat tarpeeksi, laina ei enää lyhene ollenkaan, vaan erä ei riitä välttämättä edes korkojen maksamiseen. Tällöin maksettavan määrä saattaa ruveta lisääntymään.

Lainan korko sidotaan tavanomaisesti joko ns. euribor-korkoon, tavanomaisin euribor-korko on 12 kk:n euribor. Tällöin lainaa tarkistetaan 12 kk:n välein alkaen lainan nostopäivästä. Sen päivän euribor määrittää koron vuoden eteenpäin. Euriboriin lisätään pankin marginaali, joka on tavanomaisesti n. 0,6 - 1 prosenttiyksikköä.

Toinen korkokanta on pankin viitekorko. Näissä käytetään pidempiä korkojaksoja, varsin tavallinen on viiden vuoden korkojakso. Tällöin lainan korko pysyy kiinteänä viisi vuotta.

Excel sisältää joukon funktioita, joilla voidaan laskea kätevästi erilaisia lainoihin ja muuhunkin rahoitukseen liittyviä laskutoimituksia. Nämä tehtävät liittyvät pelkästään lainan laskemiseen.

HUOM! Vaikka pankit käyttävätkin nimitystä tasaerälaina lainastaan, pankit eivät välttämättä laske kuitenkaan lyhennyksen ja koron osuutta tässä esitetyllä tavalla. Tämä tässä esitetty annuiteettimenetelmä antaa joka tapauksessa hyvän arvion lainaerän koolle. Todellisuudessa pankit laskevat lainalle koron erikseen jokaiselle päivälle.

Tehtäviä

Ohessa eräs lähtökohta lainanoton suunnittelulle:

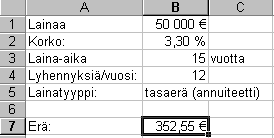
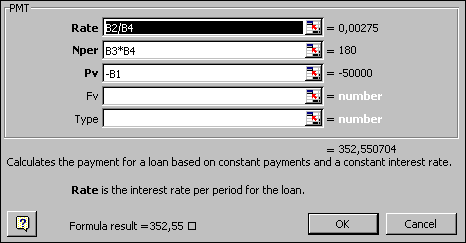
Lainaa ollaan siis ottamassa 50 000 €, koron ollessa tällä hetkellä 3,3%. Laina-ajaksi on ajateltu 15:ä vuotta ja lainaa lyhennettäisiin kuukausittain. Tällaisen lainan kuukausierän laskeminen tapahtuu maksu-nimisellä-funktiolla, (engl. PMT) jolla on seuraavat parametrit:

• Korko, joka tarkoittaa korkokauden korkoa. 3,3% on vuosikorko, ja korkokausi on tässä tapauksessa yksi kuukausi, koska lainaa lyhennetään joka kuukausi.
• Kaudet_yht, kertoo, montako lyhennystä tarvitaan, ennenkuin laina tulee maksetuksi
• Nykyarvo, eli se arvo, josta lähdetään lyhentämään. (esimerkissä 500 000 mk). Huomaa, että se pitää antaa negatiivisena! (kuvastaa sitä, että laina lyhenee)
• Ta, eli tuleva arvo-kenttää ei tarvitse täyttää. Kenttään voidaan kuitenkin kirjoittaa tarvittaessa jokin arvo, johon pyritään. Laina yleensä maksetaan kokonaan pois, joten tätä ei tarvitse lainalaskelmissa huomioida
• Laji taas kertoo, milloin laina erääntyy. Jos tähän ei laiteta mitään, laina erääntyy kuun lopussa. Näinhän asia lainoissa on: jos otetaan laina kuukauden 1. päivänä, ensimmäinen lyhennys tapahtuu vasta seuraavan kuun 1. päivänä.

1. Selvitä esim. internetiä apuna käyttäen, paljonko on tämän päivän euribor-korko. Käy myös parin pankin sivuilla tutkimassa, löydätkö pankin marginaalia.

2. Laske, paljonko lainan lyhentäjä joutuu 15:ssä vuodessa lainasta maksamaan.

3. Paljonko kuukausieräksi tulee, jos laina-ajaksi asetetaankin 30 vuotta? Paljonko tällöin lainan ottaja joutuu lainastaan maksamaan?

4. Korko nousee yhden prosenttiyksikön. Paljonko nousee kuukausierä 15:n ja 30:n vuoden tapauksissa?

5. Laadi lainalle seuraavankaltainen lyhennystaulukko koko laina-ajalle: (kuvassa on vain 8 ensimmäistä kuukautta) [HUOM! taulukossa on kaksi otsikkoa (korko ja lyhennys) väärin päin!]

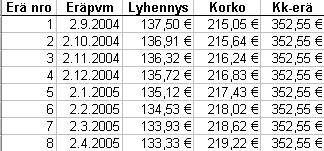
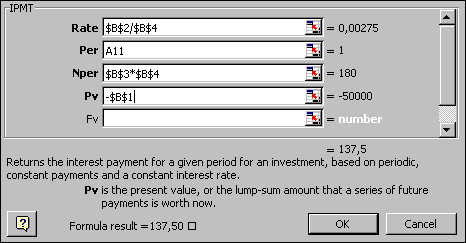
Tähän tarvitset IPMT- tai PPMT-funktioita. Näistä PPMT laskee lyhennyksen määrän annuiteetin kuukausierästä. Esimerkissä on käytetty aikaisemmin esillä olevia arvoja:

• Korko on korkokauden korko. Huomaa taas, että lainoissa ilmoitetaan vuosikorko!
• Kausi-kohtaan kerrotaan, monennenko maksuerän kohdalta lasketaan lyhennystä
• Kaudet_yht on taas lyhennyksien kokonaismäärä
• Nykyarvo-kohtaan laitetaan taas lainan määrä ja taas negatiivisena, koska laina lyhenee!

6. Mitä tapahtuu lyhennyksen osuudelle lainasta, kun lainan korko nousee prosenttiyksikön?

7. Kuinka suuri on ensimmäisessä erässä lyhennyksen osuus, kun laina-aika on 30 vuotta?

8. Paljonko lainaa on jäljellä yhden vuoden lyhennyksen jälkeen?

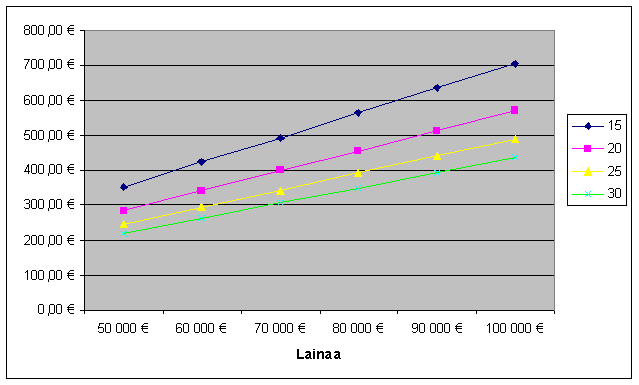
9. Haluat vertailla asuntolainoja erimittaisina ja eri lainamäärillä. Teet sitä varten seuraavanlaisen taulukon:

Laske sitten kaikki puuttuvat luvut taulukkoon.

10. Piirrä yo. taulukosta seuraavanlainen kuvaaja, jotta näkisit, miten lainojen kuukausierät käyttäytyvät:

Sivua on päivitetty 3.5.2010.